Setting

• let \(N=1591, h=0.02, \nu_2 = 0\)

• water height: \(2.96m\)

• 

Oscillation Frequency over Stiffness

• fixed \(\Delta t=\frac{1}{5000}\)
• time interval \(2s \le t \le 12s\)
• the signal is \(f(t) = \rho_{avg}(t) - \rho_0\), which measures compression
• use Fourier analysis to find:
  • peak frequency of the oscillation
  • zero frequency (total density error)

Results:

Total density error as a function of \(k\):

Oscillation peak frequency as a function of \(k\):

Interpretation:

• viscosity doesn’t change the frequency or total error in this setting
• error decreases exponentially with \(k\) (?)
• oscillation frequency increases with \(k\)
  • possible explanation: \(f \propto c\) since the oscillations move at the speed of sound \(c\)
  • Newton–Laplace equation: \(c = \sqrt{\left(\frac{\partial P}{\partial \rho}\right)}= \sqrt{\frac{k}{\rho}}\)
  • explains \(\sqrt{x}\)-shaped curve

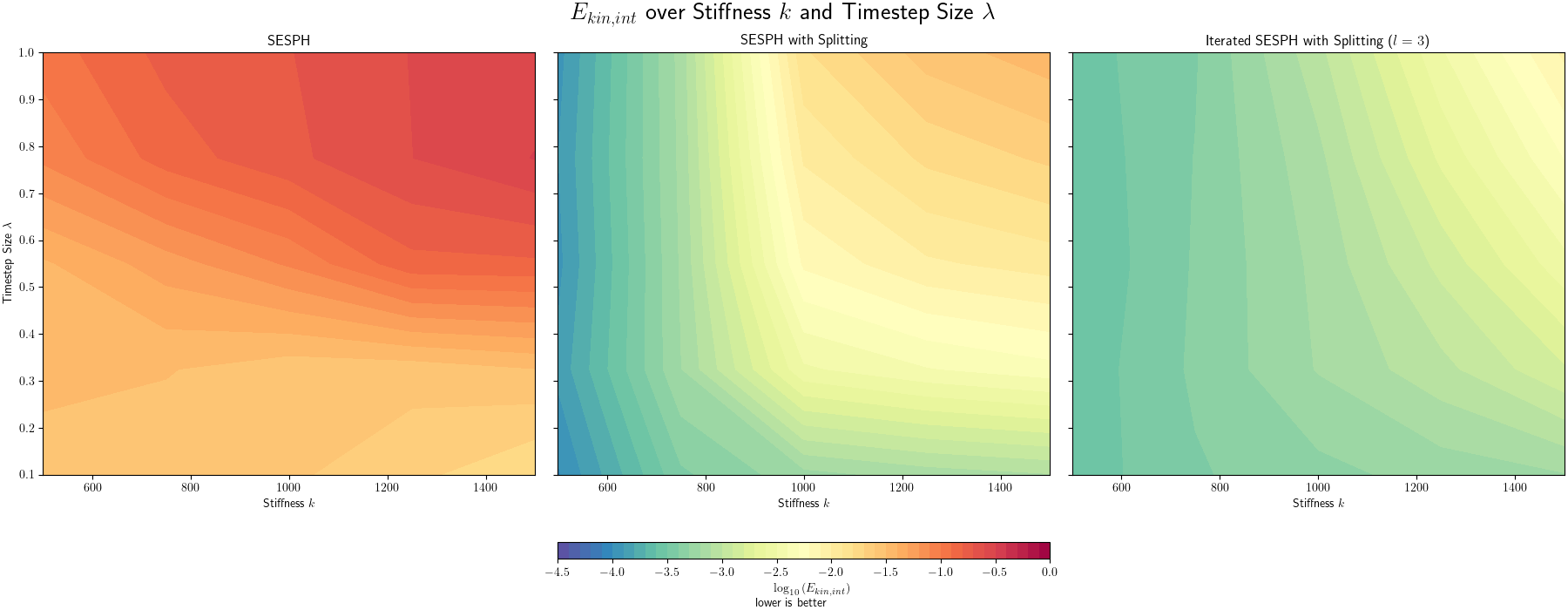
Stability over Viscosity, Stiffness and Timestep Size

• time interval: \(10s \le t \le 20s\)
• time integral of kinetic energy (less is better):
  • \[E_{kin, int} = \int_{10s}^{20s} \frac{1}{N}\sum_{i=1}^N \frac{1}{2} m_i (\vec{v}_i \cdot \vec{v}_i) \, dt\]
• peak average kinetic energy (less is better):
  • \[E_{kin, peak} = \max_{10s \le t \le 20s} \frac{1}{N}\sum_{i=1}^N \frac{1}{2} m_i \left(\vec{v}_i(t) \cdot \vec{v}_i(t)\right) \, dt\]

Fixed Timestep

• set \(\lambda = 0.1\)
• \(k\) on the x-axis, \(\nu\) on the y-axis

$$E_{kin, int}$$

$$E_{kin, peak}$$

Fixed Viscosity

• set \(\nu = 0.0001\)
• \(k\) on the x-axis, \(\nu\) on the y-axis

Results for Improved Pressure Solvers:

• new solvers help reduce error in this setting by orders of magnitude!

Video of increased stability:

• \[\nu=0.0001,\nu_2=0, \lambda = 0.1, k=1000\]
• from left to right: SESPH, SESPH with splitting, iterated SESPH with splitting