Operator Splitting:
Split up the pressure and non-pressure accelerations.
The entire algorithm is now:
- \[\rho_i = \sum_j W_{ij} m_j + \sum_k W_{ik} m_k\]
- \[a^{vis}_i = 2\nu_1(d+2) \sum_j \frac{m_j}{\rho_j} \frac{\vec{v}_{i,j}\cdot \vec{x}_{ij}}{\lVert\vec{x}_{ij}\rVert^2 + 0.01h^2} \nabla W_{ij}\]
- \[a^{adh}_i = 2\nu_2(d+2) \sum_k \frac{m_k}{\rho_0} \frac{\vec{v}_{i}\cdot \vec{x}_{ik}}{\lVert\vec{x}_{ik}\rVert^2 + 0.01h^2} \nabla W_{ik}\]
- \[a^{\text{non-pressure}}_i = a^{vis}_i + a^{adh}_i + \left(\begin{array}{c} 0\\-9.81\end{array}\right)\]
- \[\Delta t = \min\left(0.001, \lambda \frac{h}{v_{max}}\right)\]
potentially iterate \((l=3)\):
- \[\vec{v}^*_i = v_i(t) + \Delta t a^{\text{non-pressure}}_i\]
- \[\rho_i = \sum_j m_j W_ij + \sum_j m_j (\vec{v}^*_{ij} \cdot\nabla W_{ij}) + \sum_k m_k W_ik + \sum_k m_k (\vec{v}^*_{i} \cdot\nabla W_{ik})\]
- \[p_i = k \cdot \max\left(\frac{\rho_i}{\rho_0}-1, 0\right)\]
- \[a^p_i = -m_i \sum_j \left(\frac{p_i}{\rho_i^2} + \frac{p_j}{\rho_j^2}\right) \nabla W_{ij} - \gamma_2 \left(\frac{p_i}{\rho_i^2} + \frac{p_i}{\rho_0^2}\right) \cdot \sum_k m_k \nabla W_{ik}\]
- \[\vec{v}_i(t+\Delta t) = \vec{v}_i^* + \Delta t a^p_i\]
- \[\vec{x}_i(t+\Delta t) = \vec{x}_i + \Delta t \vec{v}_i(t+\Delta t)\]
- Yields the
SplitingSESPHandIterSESPHsolvers - \(\Longrightarrow\) actually massive stability improvement for low viscosity!
- \(\Longrightarrow\) lower compression
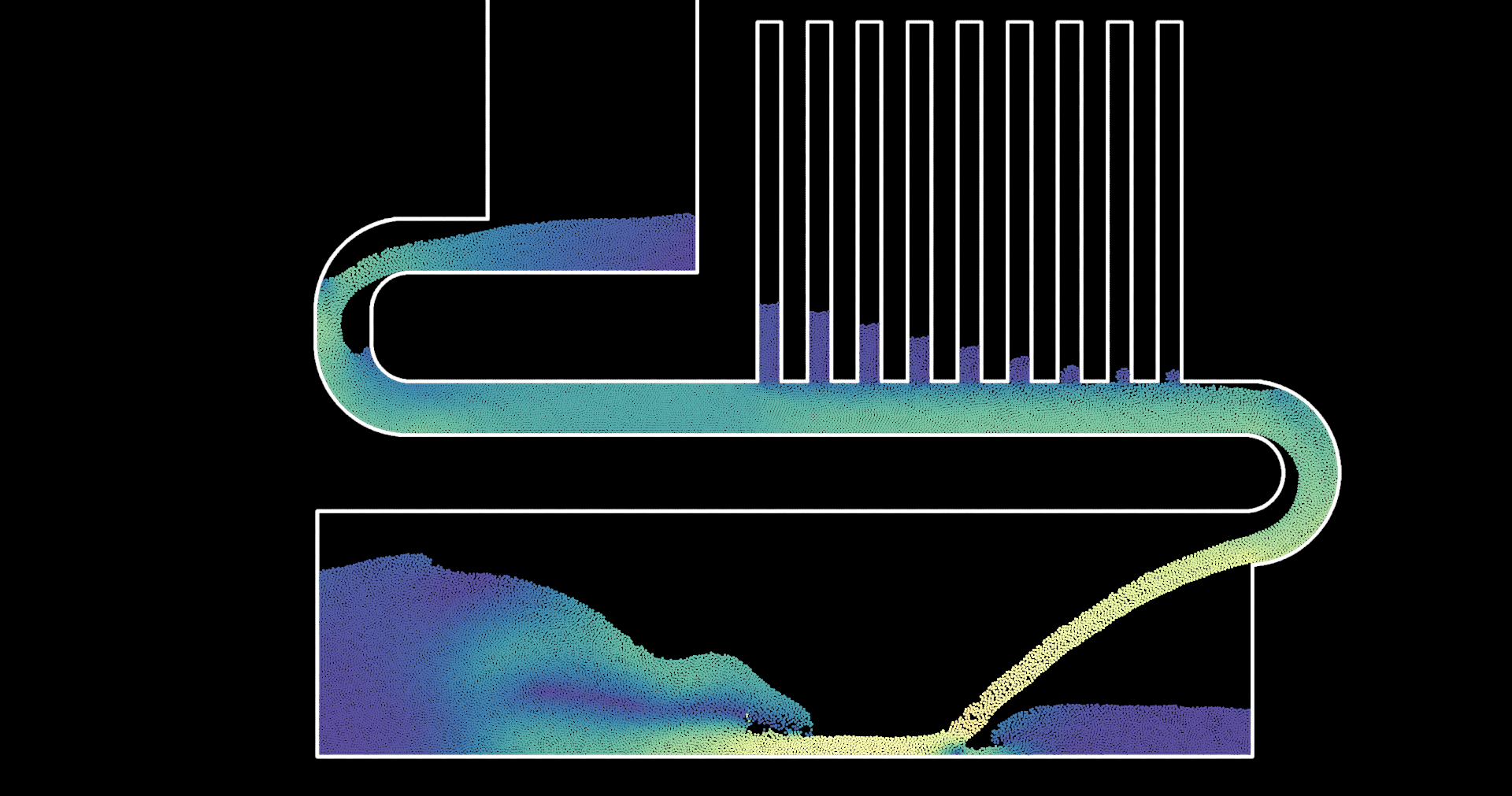
Poiseuille’s Law in action
with new pressure solver, attempt physics experiment to demonstrate the Hagen–Poiseuille equation and check plausibility
- when flow is laminar and flowrate is constant
- pressure drop \(\propto\) slope of heights \(\Delta p \propto l\cdot \nu\)
- oberservable in the small water columns
low viscosity \(\nu=0.0001, k=1000, t=7.16\): 
high viscosity \(\nu=0.2, k=2000, t=7.16\): 